Everything you need to know to use Bitcoin Cash with SeedCash

As we embark on the path to becoming a sovereign bitcoiner, we encounter various challenges. First, understanding the underlying philosophy: its economic, political, and, in my opinion, moral impact. Once we overcome these barriers, which in the case of Bitcoin are always as high as our curiosity wants to build them, we face the practical learning, its usability.

I want to distill the most important knowledge that my experience has provided me, in such a way that by the time you finish reading these few pages, you will have grasped all the necessary knowledge to use Bitcoin with confidence and understanding. This article is the 20% effort that leads to 80% of the results.

If you are an advanced user, much of the information related to "Concepts" may seem redundant. Although I recommend reading this section to reinforce or recall concepts. You can skip directly to "Explication"

Concepts

The theoretical foundation necessary to use Bitcoin with peace of mind

When we decide to exile ourselves to this parallel, free, and decentralized economy that Bitcoin allows us to access, the first step we must take is to obtain it. To get Bitcoin, to receive it, we first need a place to store it.

Later on, we will see that the verbs "send," "receive," or "store" Bitcoin are inaccurate—more precisely, incorrect—but for now, you will allow me to use them.

Let's return to our goal: storing Bitcoin. Imagine 2^256 mailboxes—hard to grasp, right? We are talking about a value equivalent to the number of atoms in the universe. Well, in Bitcoin, you have 2^256 "mailboxes" where you can store Bitcoin.

Each of these mailboxes can hold Bitcoin. Each mailbox is associated with a key (private key) that only the owner should possess (or, rather, know), and it has a sign with its address (public key). Anyone who has the key (knows the private key) can open the mailbox, "take the Bitcoin," and throw it into another mailbox with its own public and private key. In other words, if you have the key to a mailbox, you control the funds because you can spend them. Anyone who knows the address (public key) can find the mailbox and deposit Bitcoin. Similarly, they could simply wait and observe who deposits Sats into that mailbox. (The subunit of account in Bitcoin is called Sats | 1 BCH = 100,000,000 Sats)

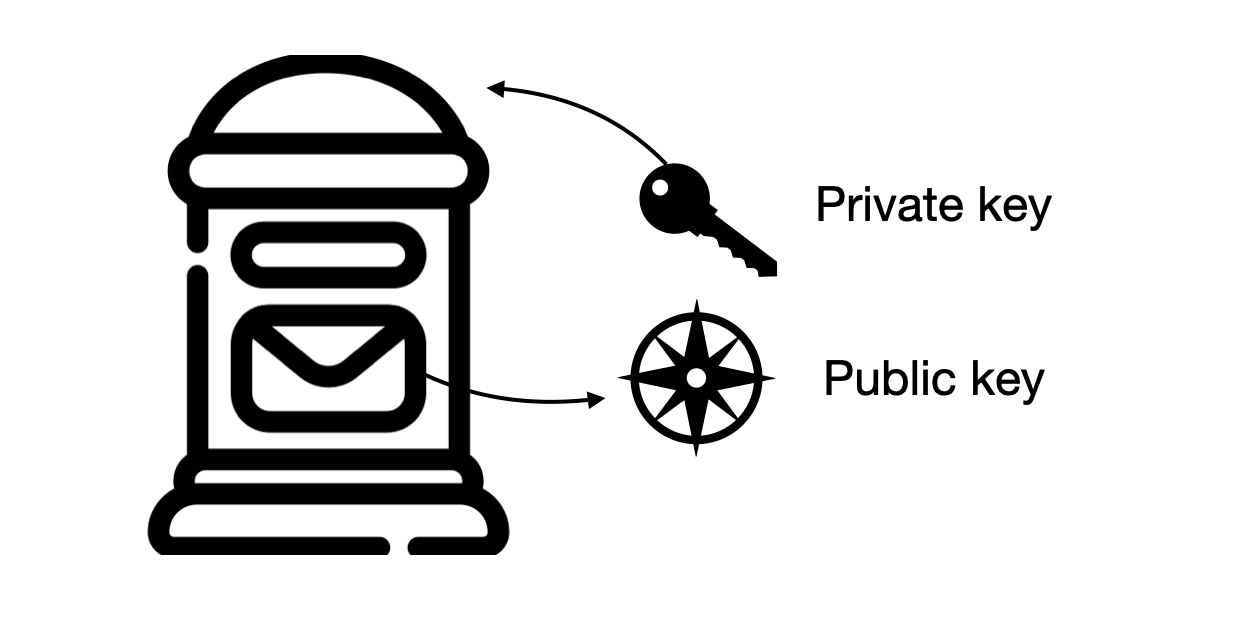
Let's be clear, without metaphors that confuse us.

A bitcoin wallet is characterized by two very important associated numbers. A private key, which is any number smaller than 2^256, and a public key, which is another number that is built from our private key. That is, to create a wallet we have to choose a number that we will call the private key (secret) and we will use this number to generate through mathematical operations another resulting number that we will call the public key (public). As we will see later, owning bitcoin is having the power to spend. To spend our bitcoins we have to use our private key to prove that said bitcoins are our property. Whoever knows a private key will have everything necessary to justify that he is the owner of some Sats and, consequently, will be able to spend said Sats. Simplifying; The public key allows you to receive and the private key allows you to spend where the private key is only known to you, and if not, another would also have control over your funds.

Let's summarize.

To store bitcoin we have to choose any number less than 2^256. This number will be our private key, our key. Anyone who knows this number will have control over the associated funds, "stored" in this private key. Using mathematical operations based on our private key, our secret number, we obtain our public number, our public key, which other bitcoiners will use to "send" us bitcoin. From the private key it is easy to generate the public key but from the public key it is not possible to generate the private key. For the more curious, bitcoin uses an elliptic curve cryptography system for this purpose.

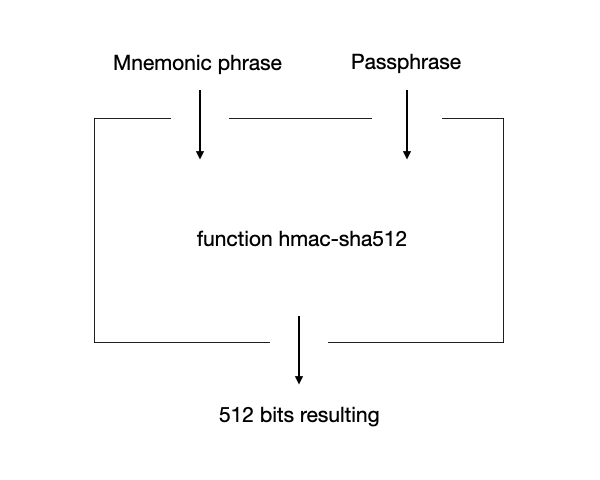
Let's understand the process by which our private key is generated. In bitcoin, as we have said, private keys are a number less than 2^256. In order for the choice of this number to be truly random and, consequently, secure, we are not going to choose it ourselves. We are going to create two elements (we will now see what elements they are) and later we will use these two elements as input for a function called hmac-sha512. That is, we take element 1 and element 2, we introduce them in the hmac-sha512 function and this function returns the result. With the previous result we will obtain the private key.

I think everything has suddenly become complicated. I am going to explain four concepts that I want you to understand before reviewing what was said above and continuing with the explanation.

What is a hash function?

A hash function is a function that takes any input value and returns a value of a certain length (for the same hash function it is always the same length) in such a way that for the same input value we will always obtain the same output, but if we slightly vary the input value the output value changes radically.

What is hmac-sha512?

For our purpose it is not necessary to understand this function in detail. Consequently, we will consider that hmac-sha512 is a hash function that takes two input values and returns one output of 512 bits (64 bytes). Remember the properties of a hash function.

How to convert from decimal to binary?

Any decimal number can be expressed in binary. Similarly, any binary code can be expressed as a decimal number. So let's see how to convert a decimal number to binary. Any decimal number can be built as the sum of powers of two. 12 = 1*2^3 + 1*2^2 + 0*2^1 + 0*2^0 → 1100 To convert 12 to binary we have to obtain the factors of the sum, in this case: 12 = 1100 For the case of 5: 5 = 1*2^2 + 0*2^1 + 1*2^0 → 101

How to convert from binary to decimal?

We are going to do the reverse process. First, let's write, from 2^0, the number of powers of two equivalent to the number of the length of our binary code (if the binary code has 0 on the left, we do not consider them). Then, for each position, if the power of that position corresponds to a 1 in the binary code, we add the value of the power of two in question. If it corresponds to a 0, we do not add it (we multiply it by 1 in the first case and by 0 in the second). Consider that when choosing the factor assigned to the power 2^0, we will look at the leftmost bit. For 2^1, the second leftmost bit, etc.

Let's look at some examples better.

Let's convert 101 to decimal: We have a binary code that is three elements long, so we need to write the first three powers of two: 1*2^2 + 0*2^1 + 1*2^0 Now we add the powers and the result is our decimal number, 5. Let's convert 0000101 to decimal: Since we have 4 leading zeros we simply ignore them and repeat the above process Let's convert 1100 to decimal: We have 4 elements, so we need the first 4 powers of two: 1*2^3 +1*2^2+0*2^1+0*2^0 = 12

Okay. Now that we understand the above concepts, we are ready to pick up where we left off. Remember: To get the private key we must create an element 1 and another element 2. We introduce the two elements as input in hmac-sha512 and we get a resulting sequence of 64 bytes, that sequence is equivalent to a sequence of 512 bits. The first 256 will be our private key. The next 256 bits are of no interest to us now. All we need to have control over a wallet is to keep under our knowledge the value resulting from the hmac-sha512 function. The first 256 will be our private key and the next 256 will be our chain code (as I said, the chain code is of no interest to us now). I insist; To have a secure wallet we need to keep our private key and our chain code under our knowledge and in a secret manner. At this point, you might be asking yourself: Ok, I need to save my private key (first 256 bits of the hmac-sh512 result) and my chaincode (second 256 of the hmac-sha512 result) but how do I get them? What were those elements we were talking about? Ok, let's get to it.

As we said, the hmac-sha512 function takes two values as input. So far we have provisionally defined them as element 1 and element 2. First of all, I want to clarify that the hmac-sha512 function does not take elements 1 and 2 directly, but rather transforms them into bytes format. Element 1 is the mnemonic phrase. Element 2 is the passphrase. For our purpose, saving bitcoin, we will have to securely generate both elements.

What is a mnemonic phrase and how to generate it?

A mnemonic phrase is a way to represent and remember (in a human-friendly way) a binary sequence. Another binary sequence is. Element 1, the mnemonic phrase is nothing more than another number less than 2^256. A number less than 2^256 that in order to remember (or save) we convert it into a mnemonic phrase. The first step to obtain our mnemonic phrase is to choose our secret number in binary, that is, a sequence of up to 256 bits.

Of course, it must be done according to the bitcoin standards (beep 39), we see them below: Our sequence can be 128,160,192, 224 or 256 bits long. Consequently, we will have 12,15,18,21 or 24 words. The standard in bitcoin is 12 or 24 words. Once we have chosen the length of our mnemonic phrase, we are going to create the corresponding bit string.

Now we have to take a piece of paper, a pen and a coin (or any other way of obtaining good entropy), toss it 128, 160, 192, 224 or 256 times and write down for each toss if the result is 0 or 1 (assign one side one value and the other the opposite). This procedure is described in detail in "Explication". Any other procedure is valid to obtain a string of 128, 160, 192, 224 or 256 bits in length as long as the method provides good entropy.

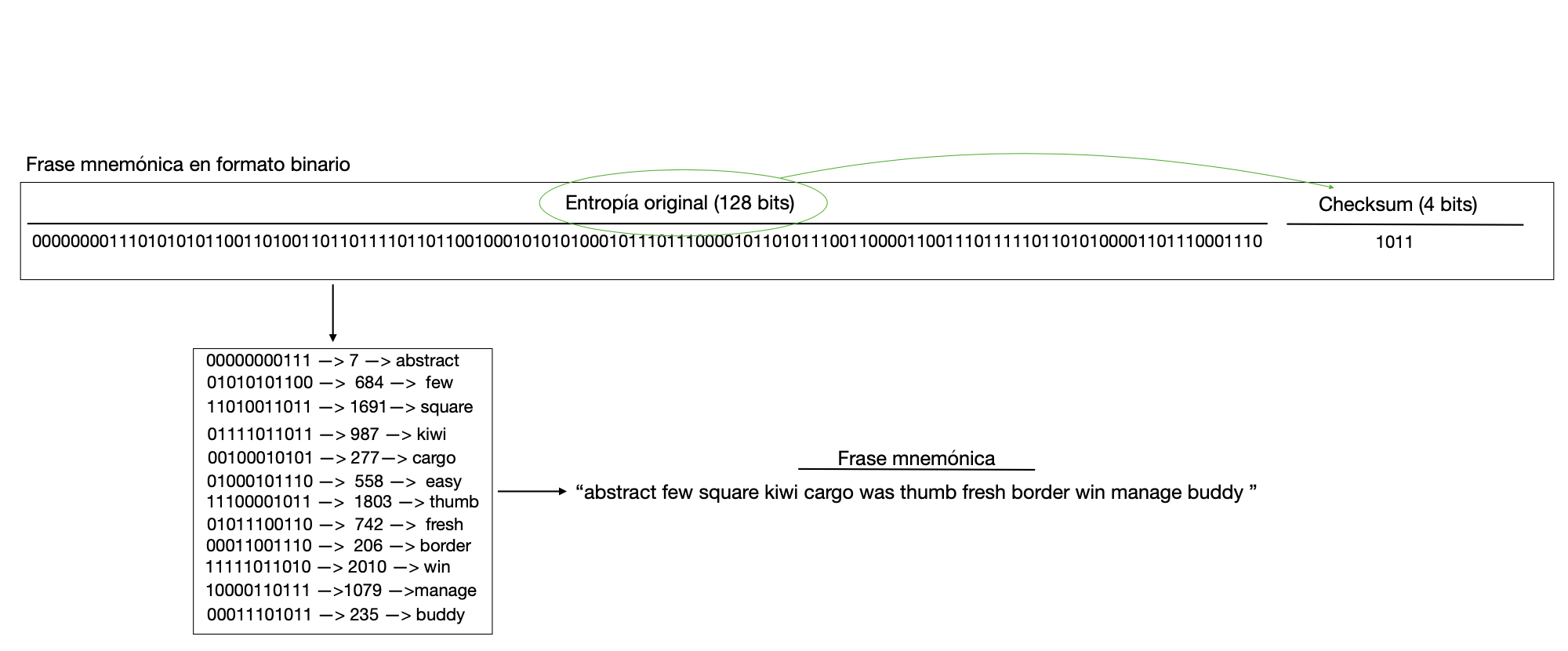
We now have a string of 128, 160, 192, 224 or 256 bits. It is still incomplete. We need to add a few bits to it. We need to add what is known as a checksum. A checksum is a "verification sum", the result of a sha256 hash of our bit string from which the first bits are extracted and added to our string. The length of the checksum, that is, the number of bits that are taken to add to our string from the result of the hash of our string, are respectively 4, 5, 6, 7 or 8.

Let's summarize a little. To our string of 128, 160, 192, 224 or 256 bits that we have made by hand, bit by bit, by tossing a coin, a die or with any other source of entropy, we have to add a few more bits, a "summary". This summary is called a checksum and is built by making a hash of the string of bits that we have made with paper and pen. The result of the hash (since sha256 is used) is 256 bits of which we are only interested in the first 4,5,6,7 or 8 depending on the length of our original bit string (taking 4 bits for the case of 128,5 for the case of 160 etc). We take the first 4,5,6,7 or 8 bits and add them to our original string of 128,160,192, 224 or 256 bits, resulting in a string of 132,165,198, 231 or 264 bits in length. Congratulations, now you have your seed, your mnemonic phrase in binary format.

But wait, if you've been paying attention, there's something that doesn't add up. To generate our original bit sequence everything has been very analog, paper and pen, you know what I mean. And suddenly you ask me to make a hash? My friend, that's a bit dificult with paper and pen. We need a computer and here the complications begin. If you take your usual computer and enter a website that has the sha256 hash function implemented, you will get the checksum quickly, but you have just compromised your seed. I dare say more, when trying to complete a checksum with any computer with the ability to connect to the Internet, you compromise your mnemonic phrase. This is where SeedCash comes in.

One of the features of SeedCash is to be able to have a computer that can never connect to the Internet. This allows you to use your private key without fear of anyone being able to access it. SeedCash has implemented the "generate seed" function where, starting from an original string of 128, 160, 192, 224 or 256 bits, it generates the checksum. But again, the operation of "generate seed" is explained in detail in "Explication". Now we focus on understanding the theoretical foundations. I am going to assume that SeedCash provides you with the checksum. Now, we have our mnemonic phrase in binary format.

Now we have to transform it into a mnemonic phrase. To do this, we will have to take our binary string and divide it into blocks of 11 bits. (I want you to notice that 132/11=12, 165/11=15 etc.). After doing the previous grouping we will have 12,15,18,21 or 24 strings, each of them with 11 bits of length. It is time to remember what we learned about how to do a binary to decimal conversion. We are going to take each of the groups of 11 bits and we are going to transform them to decimal. As a result we will get 12,15,18,21 or 24 numbers. In bitcoin we have a dictionary (Bip 39). It is a dictionary that relates a word with a number less than or equal to 2048. I want you to notice that the maximum decimal value for an 11-bit binary string is 2048. We will consider each number obtained as the index of the word in said dictionary (Bip 39) and we will keep the word that occupies the index position in question. We had obtained 12,15,18,21 or 24 groups of 11-bit strings and converted them into 12,15,18,21 or 24 numbers. Now we will obtain 12,15,18,21 or 24 words, each word corresponding to the word that occupies the position in the dictionary corresponding to the number obtained for that word. These words will be our mnemonic phrase. Now we have the first input for our hmac-sha512 function, a string of 12,15,18,21 or 24 words.

Let's look at an example.

What is a passphrase and how to generate it?

Remember that an hmac-sha512 function needs two inputs. We have created the first one, we are missing the second one. This second one is called a passphrase. A passphrase is simply a string (in programming, a string is a type of data used to represent text). It is important to consider that any slight variation in this string would result in a completely different result for our hmac-sha512 and consequently we would obtain a completely different private key and chain code. An extra space, a capital letter instead of a lowercase letter, a comma... It is very important that when you decide what your passphrase will be, you check that you have it written down correctly. With absolute accuracy. You always have the option of having a null passphrase. In that case you will only need to carefully save your recovery phrase, that is, your mnemonic phrase. Personally, I recommend using a passphrase, since it adds a lot of security at a low cost. Also consider that for the same mnemonic phrase, the use of different passphrases results in different private keys and chain codes. That is, in different "mailboxes". My example passphrase will be: "232y buka wABHGE82" Now it is your turn to create your own passphrase. You can use a more friendly string to make it easier to remember. Consider that the shorter and simpler it is, the more vulnerable your funds would be to a brute force attack in the event that an attacker obtained your mnemonic phrase and did not know the passphrase.

If this article is bringing you value, if you are learning, I encourage you to practice value for value. You will be supporting the creation of this content and the development of SeedCash.

The QR corresponds to a bitcoin cash address ( cashaddr ).

Okay, now you understand and know how to generate a mnemonic phrase and a passphrase. You know that these values will be entered into a hmac-sha512 function and the result, a 512-bit string, will be split into two parts, the first 256 bits will be the private (master) key and the second 256 bits will be the chain code (master). You will understand the "master" later.

There is one thing I would like to clarify. I said earlier that to have a bitcoin wallet you only need to keep your master private key and your master chain code secret. That is correct, but it is not done that way. As we said, if you keep your master private key and your master chain code secret you have everything you need, but it is not practical. Remember that these are two 256-bit strings. What we are going to save is the information that, when we enter it in hmac-sha512, generates the master private key and the master chain code, that is, the mnemonic phrase and the passphrase. The different bitcoin applications that you use (such as SeedCash) will take care of, starting from the entered mnemonic phrase and the passphrase, deriving the master private key and the master chain code.

Now you have everything you need to generate your bitcoin wallet. With your mnemonic phrase and your passphrase you can always get your master private key and your master chain code.

So far I have been mentioning, along with the master private key, a so-called "master chain code". Let's understand Bip32, another of the most important Bitcoin implementations.

I want to clarify that I use Bitcoin and Bitcoin Cash interchangeably.

Remember that to "receive" funds we need our public key. In bitcoin all transactions are public so that there is a record of which public key has transferred x bitcoin to another public key. To improve our privacy we might be interested in using different public keys, but that brings problems. Remember that generating and saving a seed phrase with a passphrase is not easy, it requires elaboration and saving many would not be practical. Consequently, bip32 (in bitcoin BIP is the acronym for bitcoin implementation proposal, an update) introduces the concept of HD wallets, deterministic hierarchical wallets. Let's develop this concept. Remember that our goal is to have different public keys, therefore we have to have different private keys, well. How do we achieve this? If we had a private key and any other chain of information (chain code) we could combine both binary codes to obtain infinite private keys and, consequently, innite public keys. We are not going to go into this field in depth, we will leave it for future publications, "advanced previous concepts".

I want you to keep the following in mind. With our master private key and our master chain code we can generate child private keys. These child private keys will be the ones that guard funds but we will only keep the master private key and the master code, enough information to always be able to generate the child private keys and control the funds.

Until we go deeper into bip32 in "advanced concepts" I recommend that you skip the middle step, which refers to the m/44'/145'/0' derivation path. I want you to keep the following in mind. Starting from our master private key together with our master chaincode, combining them and using hash functions we obtain practically infinite child private keys that will ultimately be the ones that will hold the funds. As long as we have possession of our master private key together with our master chaincode we will always be able to generate the child private keys and maintain control over our funds.

We have understood the structure of a bitcoin wallet. How we can get up to 2^31 private keys with just a mnemonic phrase and a passphrase. Now we need to understand how our wallet relates to the others. How can I get sats out of my mailbox and into someone else's mailbox? How can I receive sats from another wallet in my mailbox? The process is the same, it's a matter of perspective. Do you remember that I told you that in bitcoin the verbs "send", "receive" and "save" were incorrect? As I said, they serve us initially as a pedagogical measure, but now we are getting into the subject. Let's start at the end. Storing bitcoin is keeping your private keys, that is, your master private key along with your master code, that is, your mnemonic phrase along with your passphrase, under your knowledge and out of the reach of others. Remember that storing your mnemonic phrase along with your passphrase is equivalent to storing your master private key along with your master code. Of course, the standard (for practicality) is to save the mnemonic phrase and the passphrase. And now, what does it mean to send bitcoin? Or in other words, what does it mean to receive bitcoin? Let's see. A bitcoin transaction, that is, a situation where one person "sends" and another "receives" can be understood as a contract. This contract consists of different parts, "clauses". See the following diagram for the composition of a bitcoin tx.

Overwhelming, right? In this article, "Concepts", we will not address the tx from a technical and deep aspect, I just want you to have an outline of its structure. A bitcoin tx is a sequence of information and is not built all at once, it requires different steps until it has everything necessary and is ready to be introduced into a block of the bitcoin network. We could define two stages. The first step is to build a "raw tx" (also called proto transaction). A raw tx, as seen in the previous diagram, contains all the elements of a bitcoin tx, all the information necessary to define the structure of said transaction. But then what is the difference between a raw tx and a complete tx? This is where the second stage appears, the de finitive one. For a raw tx to become a valid tx, we need the owner to sign said raw tx. A signed raw tx becomes a tx ready to be sent to the network. Let's now take a closer look at the structure of a raw tx and the subsequent signing process.

As you can see in the above diagram, a raw tx is mainly composed, among other secondary elements that do not concern us now, of a series of inputs and outputs. The number of inputs and outputs will depend on the number of UTXOS you want to spend (each input corresponds to a UTXO) and the number of new UTXOS you want to generate (each output generates a new UTXO). A UTXO is the acronym for unspent transaction output, that is, a UTXO is an output that has not yet been used as an input. This part is a bit circular, so it is dificult for me to convey it. I will explain it again.

Imagine that you have bitcoin, for the moment we will not worry about how you got it. Your wallet consists of two amounts of bitcoin: an amount of 3 bitcoins from a first transaction and in a second transaction you received 0.5 bitcoins (as an example). Now imagine that you want to spend your entire balance. Let's create a raw tx for that purpose. The first step is to find out what the inputs are for the transaction we are creating (what bitcoins we want to spend). The second step (and now I'll go back to the first) is to define what the outputs are (where we want to send it). An output is a sequence of information from our transaction that defines who will be the future owner of a quantity of bitcoin (defined in the same output) and what conditions have to be met so that this amount assigned to that person can be spent. Remember that when I say "send bitcoin to a person", we are not "sending" them to "anyone" but rather we are giving control of a quantity of sats to a private key controlled by that person.

Let's recap. An output assigns a portion of the total sats value, resulting from the sum of the sats value of all the inputs (UTXOS) involved in the tx, to a certain address (to a certain other mailbox) and defines what requirements will have to be met so that this output (this new UTXO, that is, this new unspent output) can be spent by the owner of the new "mailbox". Generally, these requirements are limited to the new legitimate owner proving, when he wants to spend his new UTXOS, that he is definitely the legitimate owner (in the standard case of a ScriptPubKey P2PKH). There are more possibilities, but we will not go into such possibilities now, such as locktimes, multisigns and other situations.

Receiving bitcoin is a consequence of a third party using some UTXOS (outputs from a previous tx where the third party benefited, received bitcoin), that is, using unspent outputs (UTXOS) as new inputs in a new transaction. At the same time, it is defining new outputs, which will be new UTXOS for the beneficiary of the new transaction. In our case we would have two inputs, the first corresponding to the UTXO of 3 bitcoins and the second input corresponding to the UTXO of 0.5 bitcoins. As we have said that we wanted to send all our balance to a single address (a single mailbox), consequently, we will have a single output. I just lied to you, to generate a tx in bitcoin we always have to pay a commission for the node that includes the tx in the next block of the network. Consequently, for our case we would have the output corresponding to the node address (with the corresponding commission) and the output corresponding to our expense, by sending 3.49999 bitcoins to whomever we consider.

If this article is bringing you value, if you are learning, I encourage you to practice value for value. You will be supporting the creation of this content and the development of SeedCash.

The QR corresponds to a bitcoin cash address ( cashaddr ).

I want you to notice that a transaction is a contract. The difference between "sending" and "receiving" bitcoin is merely the role you take in that contract.

If at this point you do not fully understand how a transaction works, do not worry. I'm going to dedicate the following lines to insist on how the exchange in bitcoin works.

The process, I think I heard this metaphor from lunaticoin, is equivalent to taking coins with different face value (each coin is an input) and melt them into new coins. If we melt all the coins into one new coin, we would have one output, i.e. a new UTXO. But we can also melt two coins (two inputs) into 15 new coins (15 outputs, i.e. 15 new UTXOS). Or any other combination you can imagine. I want to emphasize that, obviously, the total value of the UTXOS, i.e. the outputs, has to be equal to the total value of the inputs for the tx to be valid. It is also important to consider that each output has its own unlocking contract, its own ScripSign. Each coin comes with its own usage contract.

A ScripSign is a script, a code, that proves that the UTXO unlocking conditions are met. A ScripPubKey is a script, a code, that sets such locking conditions.

I find it necessary to compile again. In order to move bitcoin we have to present a valid contract to a miner. This valid contract is a bitcoin transaction that will be included, by said miner, in a block of the chain, of the network. This bitcoin transaction consists of melting one or several coins where each one has its face value in one or several new coins with its corresponding face value. This contract is built in two steps. First, a raw tx is generated. A raw tx is a sequence of information that contains the information about which UTXOS are to be spent (inputs) and which UTXOS will be generated at the cost of such inputs (outputs). It is important to consider that the outputs not only contain the information corresponding to the amount of bitcoin and to whom such amount is directed, but they also contain the information that describes: under what conditions the new outputs can be converted into inputs for a future tx, that is, they contain the necessary information that describes the conditions that must be met so that the new UTXOS can be spent, said information, said "requirements" are known as ScriptPubKey. Now we understand how a raw tx is built. We just need to understand how to convert this raw tx into a tx ready to be sent to a node. Before that, I would like you to reread and on what has been said up to this point. Also review the diagram regarding the structure of a raw tx and the composition of each input and output.

Now that we have our raw tx in hand, let's sign it. Do you remember what we have learned about the composition of outputs? An output contains 3 blocks of information. The first contains the value in sats of said output. The second contains the size of the ScriptPubkey in bytes, and finally the ScriptPubKey where the ScriptPubKey are the requirements that are defined so that the output in question, the new UTXO, can be used as an input, that is, spent. I also want you to remember that, as I said, the most common ScriptPubKey (P2PKH) is limited to ensuring that whoever spends a UTXO is really the owner. Well, taking this into account, you can already guess what we are missing. We have our raw tx with some inputs that have not yet been completed, that is, they have not satisfied the validation conditions, they have not satisfied the ScriptPubKeys of the outputs from which they come. In other words, the ScriptSign section, the section of the input intended for the signer to attach the proofs that satisfy the spending conditions, is empty. Since we have already built our outputs and all the other parts of the tx that do not interest us now, we only need to build the information that will be attached to each ScriptSign of such inputs, that is, satisfy the ScriptPubKeys of the UTXOS to be spent.

To satisfy the ScriptPubKey of the UTXOS to be spent and complete the tx, we will have to understand what conditions are requested in the ScriptPubKey. As we said before, we are going to focus on the most common situation, a standard tx. In a standard tx (P2PKH), the ScriptPubKey of each UTXO asks us that the ScriptSign section of the corresponding input contains a cryptographic signature of the raw tx (*1). To obtain the signature we use our daughter private key corresponding to the "mailbox" where we store the UTXO to spend. We attach the public key corresponding to the private key that made the signature after the signature. The resulting sequence will be our scripsign. By iterating the process for each input we prove that we are the legitimate owners of each input (UTXO to spend). Now, having completed all the ScripSigns so that they satisfy the conditions of all the ScriptPubKeys corresponding to each UTXO to spend (to each input) we already have a valid transaction ready to be sent to the network.

*1 The procedure for signing (in the P2PKH standard) is more complex. The raw tx is taken, all the ScriptSign sections are emptied (we have a ScriptSign section for each input).

For each input of the raw tx (or proto transaction) we will iterate the following steps are followed:

1: Introduce the scriptPubKey corresponding to the UTXO to be spent on that input into the empty space of the ScriptSign of the input to be signed.

2: We will call the sequence obtained from step 1 serialized_tx.

3: hash_to_sign=sha256(sha256( serialized_tx + SIGHASH_ALL ))

4: The hash_to_sign is signed using ECDSA

5: For our input number i, the ScriptSign_i = signature + pubKey(corresponding to the privateKey that made the signature)

Finally, we take our initial raw tx to which we had emptied the ScriptSigns and in each empty section we add the corresponding ScriptSign_i. The resulting sequence is our final signed tx.

Don't worry if you haven't understood how a transaction works. It's a bit complex. What I am interested in is that you understand the metaphor of melted and subsequently minted coins, that is, how the UTXO-based transaction model works.

If this article is bringing you value, if you are learning, I encourage you to practice value for value. You will be supporting the creation of this content and the development of SeedCash.

The QR corresponds to a bitcoin cash address ( cashaddr ).

Finally, to close this article, I want to introduce you to a very important concept: that of "watch only" wallets. This concept will be a pillar, a central node in our standard security scheme that we will explain in "How to use SeedCash", our practical guide to using Bitcoin cash. Let's see what a watchonly wallet is and what it allows us to do, but first let me introduce you to two concepts that are necessary to understand what a watchonly wallet is. They will also be useful in your security scheme. Let's see what an xpriv and an xpub are.

The terms xpriv and xpub come from "extended private key" and "extended public key" respectively. Both are sequences of information that contain the master chain code and respectively the master private key or the master public key, that is, the public key corresponding to the master private key. With an xpriv we have the necessary information to control the funds in a wallet, to control a mailbox. With the xpriv we can generate a wallet and with the xpub we can do something even more interesting.

I want you to remember beep 32. Beep 32 describes the structure of Bitcoin wallets. With a master private key and a master chaincode, we could combine them to generate up to 2^31 child private keys with their corresponding child public key, and it was these child keys that held the funds. That is, to obtain the child private keys we would combine the master private key with the master chaincode and an index and we would obtain the child private key corresponding to that index. Now, here's the interesting part. With the master public key together with the master chaincode, we can generate all the child public keys. That is, for a key index (for example, suppose we want to generate the child private key number 35) if we know the master chain code and the master private key we can generate said child private key without problem and knowing the child private key 35 we can without any problem generate the child public key 35. Well, knowing the same master chain code and the master public key derived from the master private key, we can also generate said child public key 35 by combining the master chain code with the master public key. Index 35 is an example, it clearly works for all indexes (less than 2^31).

Let's summarize, if we know an xpriv we can generate an entire wallet with each of its child private keys with their corresponding child public keys. If we know an xpub we can generate all the child public keys. This is very powerful, I mean the use of an xpub, since it allows us to generate a watchonly wallet, that is, a wallet with which we can only view our balance, in which UTXOS are distributed, we can generate raw tx (unsigned) and we can use the public keys to generate addresses and receive bitcoin. I repeat, with an xpub we can generate a watchonly wallet. A watchonly wallet allows us to see the balance of our wallet and of each child public key (see all our UTXOS), generate addresses to receive bitcoin and prepare transactions that only need to be signed to be able to be sent to the network. Powerful right? The use of our xpub will be essential to generate our watchonly wallet and our watchonly wallet will be the center of our security scheme to store and use bitcoin (explained in "Explication").

Finally, I want to introduce one more concept, that of address. If you noticed the last paragraph for receiving bitcoin, I didn't say to use one of our child public keys directly, but with that child public key we generate an address. Ok, let's understand this point. Addresses are used instead of using the public key directly to improve security, privacy and usability. Let's look at the main reasons. First, we have privacy. Addresses are hashes of public keys. This means that although addresses are related to public keys, they don't reveal the full public key until it is used in a transaction. This offers an additional layer of privacy as the public key is only revealed when the transaction is committed (remember that the public key has to be added along with the signed tx hash in the ScripSign section). Second, we have security. If the public key were used directly, an attacker with a quantum computer could theoretically calculate the private key from the public key. By using an address, which is a hash of the public key, it becomes much more dificult for an attacker to attempt to derive the private key until the transaction is signed and transmitted. Finally, add that Bitcoin addresses are designed to be shorter and easier to handle compared to public keys. It is to make it easier for users to copy, paste, and type addresses without errors, and for systems to verify them more easily. Addresses also include a verification mechanism (which we've seen before) called a checksum, which helps detect typos. This is especially useful to avoid sending funds to the wrong address due to human error.

In BCH we have two kinds of addresses. The original ones in bitcoin: Legacy and the current standard: CashAddr.

1: Legacy

It is characterized by the prefix 1 or 3. The prefix 1 is used in the case of P2PKH tx and 3 in the case of P2SH. Example: 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa

2: CashAddr

It contains the header: "bitcoincash:". It is characterized by the prefix q or p. The prefix q is used in the case of P2PKH tx and p in the case of P2SH. Example: bitcoincash:qqeht8vnwag20yv8dvtcrd4ujx09fwxwsqqqw93w88

If you have made it this far, I congratulate you . This article is a large part of the knowledge I have acquired over the last 2 years about bitcoin. Knowledge that I have condensed and synthesized for you. I hope that this article has been useful to you and is just the beginning of your journey down the bitcoin rabbit hole . I recommend that you use this article not as a casual read, but as "notes" to go through and reread. This article aims to synthesize a lot of knowledge; this implies that it is dificult for the reader to digest it. I insist that you reread and complement with other sources the aspects that have been more dificult for you to understand.

If this article has brought you value, if you have learned, I encourage you to contribute to this project. You will be promoting the development of SeedCash and the writing of educational articles like the one you just enjoyed. I also invite you to participate in the SeedCash Telegram community where you will find help for everything you need, you can give feedback on the tool and even contribute to its development.

Now that we have studied the theoretical part, let's start building!